SCPC 2024 Round 1 (1차 예선) 풀이 ( KOR )
SCPC ( Samsung Collegiate Programming Cup ) 2024 Round 1 모든 문제 풀이
1. A보다 B가 좋아
1.1 아이디에이션
- 입력 크기를 보니 시간 복잡도가 O(N)이고 이중 반복문은 불가능하다.
- 구간을 최대한 작게 쪼개서 생각해볼 수 있나?
1.2 해결법
전체 문자열에서 ‘A’가 0개 일 때, 1개 일 때, 2개 일 때, 3개 일 때 천천히 예제를 만들어 보면서 규칙을 알 수 있다.
고려해볼 구간을 작게 작게 최대한 쪼개보자. 고려해볼 최대 작은 구간은 A(B..)A 같은 2개의 A에 B만 껴있는 구간이다.
두 개의 ‘A’ 사이에는 무조건 2개 이상의 ‘B’가 있으면 문제 조건을 만족한다.
문자열을 돌면서 2개의 ‘A’ 사이에 B가 몇 개인지 세고, 2개 미만이면 ‘B’가 2개가 되도록 한다.
ABBABBA 라는 문자열이 있다고 가정할 때, 첫 번째의 A와 네 번째의 A, 네 번째의 A와 일곱 번째의 A를 비교하면 된다.
굳이 첫 번째의 A와 일곱 번째의A는 비교하지 않고 양 옆으로 가장 가까운 A끼리만 비교하면 된다.
1.3 코드 보기
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include <bits/stdc++.h>
using namespace std;
void solve(){
int n;
string a;
scanf("%d",&n);
cin>>a;
int last=-1;
int ans=0;
for(int i=0;i<a.size();i++){
if(a[i]=='A'){
if(last==-1) last=i;
else{
ans+=max(2-(i-last-1),0);
last=i;
}
}
}
printf("%d\n",ans);
}
int main(){
int t;
scanf("%d",&t);
for(int i=1;i<=t;i++){
printf("Case #%d\n",i);
solve();
}
}
2. 배달
2.1 아이디에이션
- 시간 복잡도가 O(N) 아니면 힘들 것 같다.
- |d - c| + |c - b| + |b - a| + |d - a| 수식을 좀 더 간단히 정리 가능한가?
2.2 해결법
a, b, c ,d 가 오름차순이라고 가정하면 2*(d-a)로 깔끔하게 정리됨을 알 수 있다.
핵심은 그러면 a랑 d를 뭘로 선택하는 지가 핵심이다.
2*(d-a) 값들의 합이 최대가 되려면 a는 젤 작은 (n/4)개 중 하나이고, d는 젤 큰 (n/4)개 중 하나이다.
2.3 코드 보기
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
void solve(){
ll i,ans=0,n;
scanf("%lld",&n);
vector<ll> a(n);
for(i=0;i<n;i++){
scanf("%lld",&a[i]);
}
sort(a.begin(),a.end());
for(i=0;i<n/4;i++){
ans-=a[i];
}
for(i=n/4*3;i<n;i++){
ans+=a[i];
}
printf("%lld\n",ans*2);
}
int main(){
ll T;
scanf("%lld",&T);
for(ll i=1;i<=T;i++){
printf("Case #%lld\n",i);
solve();
}
}
3. 보안망 점검
3.1 아이디에이션
- 그래프가 원형이라는 것은 굉장히 특별한 조건이다.
- 원형을 이루지 않는 선, 원형을 이루는 선 각 각 하나씩 지워도 항상 모두 연결되어 있다.
- 그럼 원형을 이루는 선 2개를 지우는 것이 필요 조건인가?
3.2 해결법
degree가 3인 정점은 2개 이고, 해당 두 정점이 원형이 아닌 간선 양 끝점이다. 원형을 이루지 않은 선을 쭉 연장해서 직선으로 그어보자. 그러면 2개의 영역이 나뉘고 각 영역에서 아무렇게 2개의 간선을 뽑으면 항상 고립되는 구간이 생긴다.
3.3 코드 보기
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll ans,sv;
void dfs(ll v,vector<bool> &visited,vector<vector<ll>> &V,vector<ll> &st){
visited[v]=true;
++ans;
if(st[1]==v) sv=ans;
for(auto to:V[v]){
if(v==st[0] && to==st[1]) continue;
if(v==st[1] && to==st[0]) continue;
if(!visited[to]) dfs(to,visited,V,st);
}
}
void solve(){
ll n;
scanf("%lld",&n);
vector<ll> ind(n+10);
vector<vector<ll>> V(n+10);
vector<ll> st;
vector<bool> visited(n+10);
for(ll i=1;i<=n+1;i++){
ll x,y;
scanf("%lld %lld",&x,&y);
ind[x]++;
ind[y]++;
V[x].push_back(y);
V[y].push_back(x);
}
for(ll i=1;i<=n;i++){
if(ind[i]==3) st.push_back(i);
}
ans=0;
dfs(st[0],visited,V,st);
ll a=sv-1,b=n-a;
printf("%lld\n",a*(a-1)/2+b*(b-1)/2);
}
int main(){
ll T;
scanf("%lld",&T);
for(ll i=1;i<=T;i++){
printf("Case #%lld\n",i);
solve();
}
}
4. 딱 맞게
투 포인터, priority queue
4.1 아이디에이션
- \(O(NlogN)\) 의 시간복잡도로 풀어야하는 것이 입력 크기 조건에서 보인다.
- 어떻게 매칭되는 지 \( F(A,B)\) 가 정해져 있다고 하고, 매칭 형식을 이렇게 \((a_i,b_j )\) 표현해보자. \(maxF(A,B) = |a_i-b_j|\)\(\quad (1 \leq i \leq n \, \text{and} \, 1 \leq j \leq n)\) 가 되는 \((i,j)\) 쌍은 하나여도 충분하다. 나머지 \((i,j)\) 쌍들은 차가 \(maxF(A,B)\)이하만 만족한다면 어떻게 매칭되어도 문제가 없다.
- 이왕이면 나머지 \((i,j)\) 쌍들에 대해 \(maxF(A,B)\)가 최소가 되도록하는 재조합이 있는가?
4.2 해결법
4.2.1 보조 정리1
4.2.2 보조 정리2
길이가 n이고, 각 각 오름차순으로 정렬되있는 배열 A,B에 대해 \(maxF(A,B)\) 가 최소가 될려면, \(F(A,B)\) 함수는 모든 i에 대해 \(F(a_i)=b_i\) 다. ( \(1 \leq i \leq n\) )
4.2.3 풀이
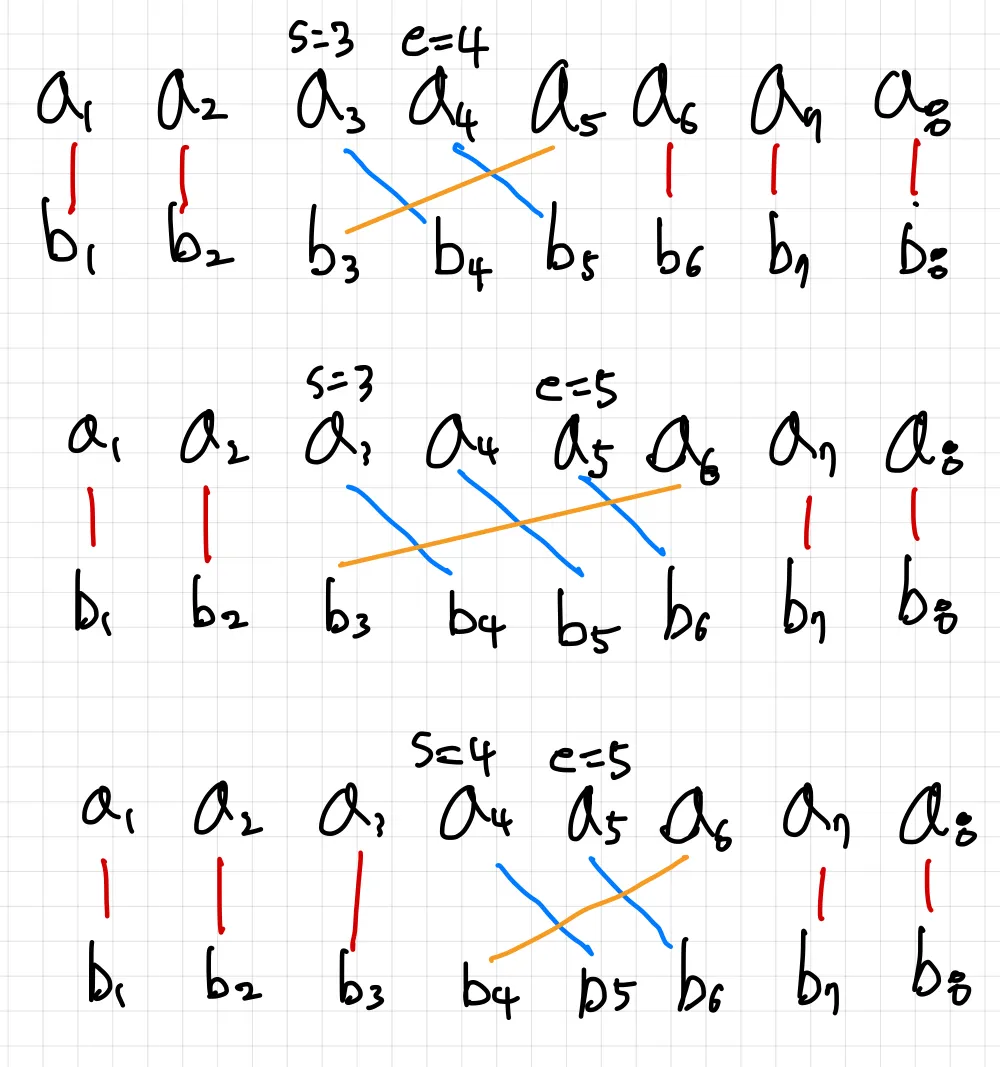
\(A\), \(B\) 배열을 오름차순으로 정렬하고, 투 포인터로 문제를 진행하자. 투 포인터 \(s\), \(e\)의 정의는 아래 그림을 보면 이해가 갈 것이다.
\(maxF\)의 값은 특정 하나의 쌍 \(a_i\) 와 \(b_j\)에 의해 결정되어도 충분함을 알 수 있다. 그리고 나머지 \(a\), \(b\)들의 차를 최소로 하려면 보조정리 2에 의해 작은 순서대로 서로 하나씩 매칭해줘야 한다. 그림 상에서는 주황 간선에 의해 \(maxF\)가 결정된다.
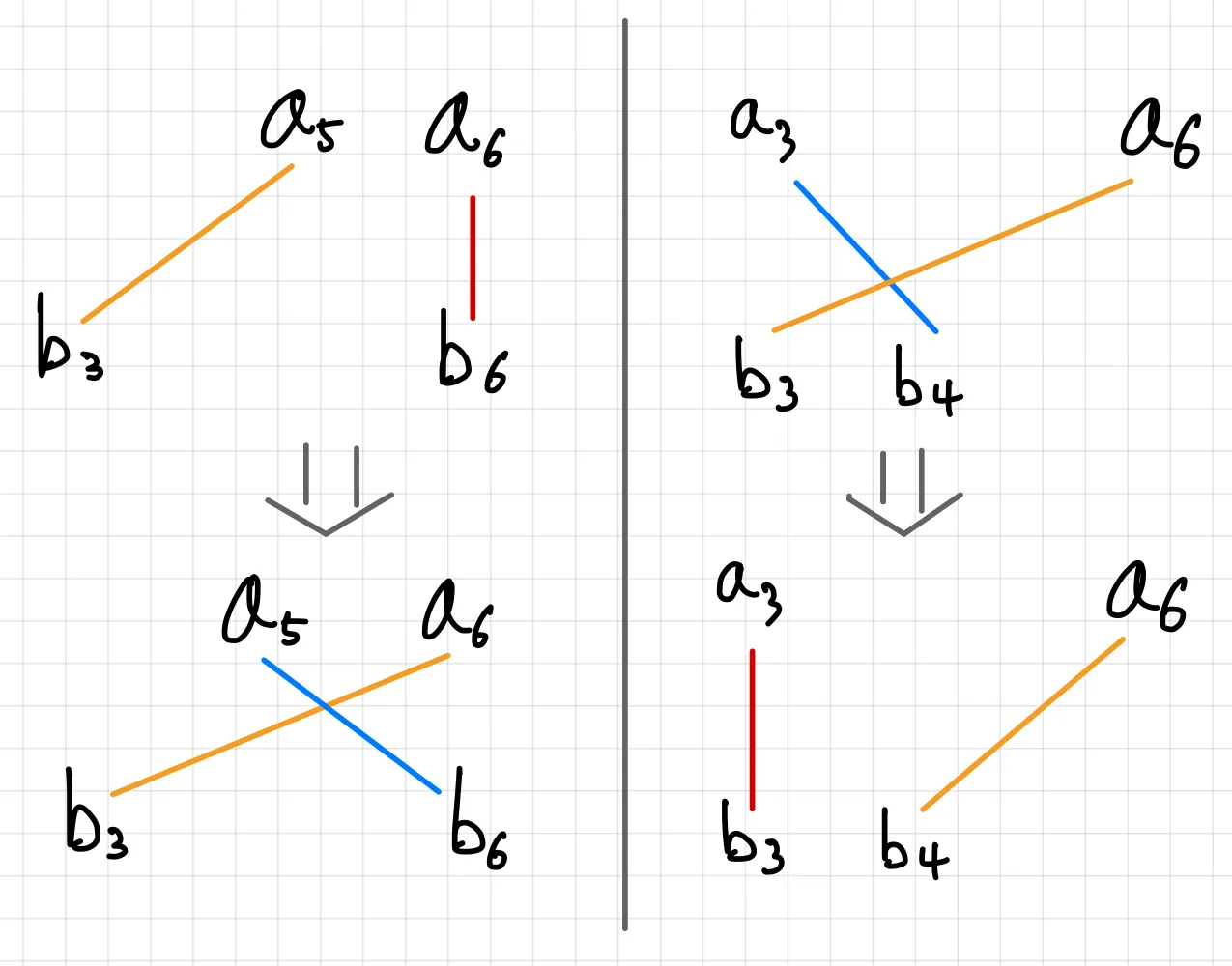
또한, ( 투 포인터가 \([s_1,e_1]\)일 때 \(maxF\) ) \(\geq\) (투 포인터가 \([s_2,e_2]\)일 때 \(maxF\)) \((s_1 \leq s_2 \text{ and } e_2 \leq e_1)\) 가 성립함을 알 수 있다. 이해가 안 된다면, 한 단계가 진행될 때 실제로 매칭이 변경된 간선들만 따로 빼서 정리한 아래 그림을 봐보자.
변화 과정에서 4개 요소들의 매칭 관계가 변경되고 이 4개 요소들에 대해 보조 정리1 적용해보면 이해가 될 것이다.
따라서, 해당 투 포인터에 대해 \(maxF\)가 \(L\)이하면 \(e\)가 1 증가, 초과면 \(s\)가 1증가. 그럼 투 포인터가 진행될 때, 해당 구간의 \(maxF\) 값을 구하고, 갱신하는 것이 핵심으로 보인다. 이 부분은 prioirity queue를 이용해 해결했다. 투 포인터를 진행하면서 \(a_i\)와 \(b_{i+1}\)의 차를 priority queue에 집어넣고, 차의 최댓값을 알고 싶을 때, priority queue의 top으로 최댓값을 알수 있다. 만약 top이 \(s\), \(e\) 구간 밖에 해당하는 값이라면 아닐 때까지 prioirity queue의 top을 pop 한다. \(maxF\)를 결정하는 \(a_i\)와 \(b_j\)에 대하여 (\(i \geq j\))일 때 차만 비교 할 것이 아니라 (\(i \leq j\))일 때 차도 고려해야 하는데, 이건 \(A\),\(B\) 배열을 바꿔서 똑같은 과정을 한 번 더하면 쉽게 해결된다. 총 시간 복잡도는 \(O(NlogN)\)
4.3 코드 보기
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
#include <bits/stdc++.h>
typedef long long ll;
using namespace std;
priority_queue<pair<ll,ll>> Q;
ll oo=9999999999L;
ll ans=-1;
void twoPointer(ll n,vector<ll> &A, vector<ll> &B, vector<ll> &maxStFromLef, vector<ll> &maxStFromRig, ll L, vector<ll> &rigM){
ll left=0,right =-1;
while(!Q.empty()) Q.pop();
while(true){
ll mx=-oo;
mx=max(mx,A[right+1]-B[left]);
mx=max(mx,left-1<0 ? 0:maxStFromLef[left-1]);
mx=max(mx,right+2>=n ? 0:maxStFromRig[right+2]);
while(!Q.empty()){
auto t=Q.top();
if (t.second<left) Q.pop();
else break;
}
if(!Q.empty()){
auto t=Q.top();
mx=max(mx,t.first);
}
if(mx>L){
left++;
if(left>right+1) break;
} else{
if(mx<=L && mx>ans) ans=mx;
right++;
if(right==n-1) break;
Q.push({rigM[right],right});
}
}
}
void preProcessing(vector<ll> &A, vector<ll> &B, ll n,ll m){
vector<ll> stM(n); // |a_i-b_i|
vector<ll> lefM(n); // |a_i-b_(i-1)|
vector<ll> rigM(n); // |a_i-b_(i+1)|
vector<ll> maxStFromLef(n);
vector<ll> maxStFromRig(n);
for(ll i=0;i<n;i++){
stM[i]=abs(A[i]-B[i]);
if(i>=1) lefM[i]=abs(A[i]-B[i-1]);
if(i<n-1) rigM[i]=abs(A[i]-B[i+1]);
}
maxStFromLef[0]=stM[0];
for(ll i=1;i<n;i++) maxStFromLef[i]=max(maxStFromLef[i-1],stM[i]);
maxStFromRig[n-1]=stM[n-1];
for(ll i=n-2;i>=0;i--) maxStFromRig[i]=max(maxStFromRig[i+1],stM[i]);
twoPointer(n,A,B,maxStFromLef,maxStFromRig,m,rigM);
}
void solution(){
ll n,m;
scanf("%lld %lld",&n,&m);
vector<ll> A(n);
vector<ll> B(n);
for(ll i=0;i<n;i++) scanf("%lld ",&A[i]);
for(ll i=0;i<n;i++) scanf("%lld",&B[i]);
sort(A.begin(),A.end());
sort(B.begin(),B.end());
ans=-1;
preProcessing(A,B,n,m);
preProcessing(B,A,n,m);
printf("%lld\n",ans);
}
int main(){
ll T;
scanf("%lld",&T);
for(ll i=1;i<=T;i++){
printf("Case #%lld\n",i);
solution();
}
}
5. 스퀘어
투 포인터, Mo’s algorithm
5.1 아이디에이션
- 배열 길이가 최대 50000이므로 아무리 50001 이상의 숫자는 아무리 모아도 자기 자신을 square 할 수가 없다. 배열에서 50001이상의 숫자는 몇 개 있는지 무시하자.
- 알면 풀고, 모르면 못푸는 전형적인 문제. Mo’s algorithm을 알아야 풀 수 있다.
- 아슬아슬하게 시간 복잡도 \((Q+N)\sqrt{N}\)로 가능할 것 같다
5.2 해결법
Mo’s algorithm을 공부 먼저 하자. 해당 알고리즘을 알고 있다는 가정하에, 투 포인터를 가지고 진행해야 하는 것이 감이 올 것이다.
s는 현재 구간의 시작 지점 인덱스, e는 현재 구간의 끝 지점 인덱스. 현재 구간에서 스퀘어가 가능한 갯수는 currentSqCnt 변수를 조회해 알 수 있다 하고, a[i]의 값의 갯수는 count[ a[i] ]를 조회해 알 수 있다고 하자.
s과 e가 하나씩 움직일 때마다 count 배열과 currentSqCnt를 갱신한다면, s, e가 바뀌어도 올바른 count 배열과 currentSqCnt를 알 수 있다. count 배열과 currentSqCnt를 갱신하는 것은 상수 시간만에 가능하다.
갱신이 상수 시간만에 가능하다는 것을 2로 예시를 들어보자. 2가 스퀘어 된다고 가정해보자.
2 * 2 = 4
4 * 4 = 16
16 * 16 = 256
256 * 256 = 65536
65536은 50000보다 크므로 무시
2가 스퀘어 될 때 영향을 미치는 숫자들은 2, 4, 16, 256이고 이 숫자들에 관련된 count 배열만 업데이트한다. 4 정도면 상수 시간이라고 봐도 무리 없다.
5.3 코드 보기
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
#include <bits/stdc++.h>
#define Limit 50000
typedef long long ll;
using namespace std;
ll k; // bucket size
struct Query{
ll s,e,index,ans;
};
bool compareByBucket(Query& lef,Query& rig){
return (lef.s-1)/k<(rig.s-1)/k || ( (lef.s-1)/k==(rig.s-1)/k&& lef.e<rig.e );
}
bool compareByIndex(Query& lef,Query& rig){
return lef.index<rig.index;
}
void updateWhenErase(ll num, ll ¤tSqCnt,vector<ll> &count){
if(num==1) return;
ll cur=num;
vector<ll> history;
while(1){
if(cur>Limit || count[cur]>0){
if(cur<=Limit) count[cur]--;
for(auto temp:history)count[temp]=temp-1;
currentSqCnt-=history.size();
break;
}
history.push_back(cur);
cur=cur*cur;
}
}
void updateWhenInsert(ll num, ll ¤tSqCnt,vector<ll> &count){
if(num==1) return;
ll cur=num;
vector<ll> history;
while(1){
if(cur>Limit || count[cur]+1<cur){
if(cur<=Limit) count[cur]++;
for(auto temp:history) count[temp]=0;
currentSqCnt+=history.size();
break;
}
history.push_back(cur);
cur=cur*cur;
}
}
void solution(){
int n;
scanf("%lld",&n);
vector<ll> a(n+1);
for(ll i=1;i<=n;i++){
scanf("%lld",&a[i]);
}
ll Q;
scanf("%lld",&Q);
vector<Query> queries(Q);
for(ll i=0;i<Q;i++){
scanf("%lld%lld",&queries[i].s,&queries[i].e);
queries[i].index=i;
}
for(k=1;k*k<n;k++); //find bucket size
sort(queries.begin(),queries.end(),compareByBucket); // sort
vector<ll> count(Limit+10);
for(ll i=queries[0].s;i<=queries[0].e;i++){
if(a[i]<=Limit) count[a[i]]++;
}
ll currentSqCnt=0,s,e;
for(ll i=2;i<=Limit;i++){
ll upCnt=count[i]/i;
count[i]%=i;
currentSqCnt+=upCnt;
if(i*i<=Limit)
count[i*i]+=upCnt;
}
s=queries[0].s,e=queries[0].e;
queries[0].ans=currentSqCnt;
for(int i=1;i<queries.size();i++){
auto query=queries[i];
while(s<query.s) updateWhenErase(a[s],currentSqCnt,count),s++;
while(s>query.s) updateWhenInsert(a[s-1],currentSqCnt,count),s--;
while(e>query.e) updateWhenErase(a[e],currentSqCnt,count),e--;
while(e<query.e) updateWhenInsert(a[e+1],currentSqCnt,count),e++;
queries[i].ans=currentSqCnt;
}
sort(queries.begin(),queries.end(),compareByIndex);
for(auto query:queries) printf("%lld\n",query.ans);
}
int main(){
ll T;
scanf("%lld",&T);
for(ll i=1;i<=T;i++){
printf("Case #%lld\n",i);
solution();
}
return 0;
}