Maximum Bipartite Matching

1. Bipartite Graph

If you can paint all vertices of a graph in two colors such that adjacent vertices have different colors, the graph is called a bipartite graph.

2. Maximum Bipartite Matching

Maximum Bipartite Matching is an algorithm used to find the maximum matching in a bipartite graph.

So, what is maximum matching?

A matching in a graph is a set of edges such that no two edges share a common vertex. In other words, it is a way of pairing up vertices such that each vertex is connected to exactly one other vertex via the edges in the matching.

In a bipartite graph, the goal of the maximum bipartite matching algorithm is to find the largest possible matching, where the number of paired vertices is maximized. This means identifying the maximum number of edges that can be included in the matching without any two edges overlapping on a same vertex.

The algorithm is particularly useful in various practical applications, such as job assignments, where tasks need to be assigned to workers in a way that maximizes efficiency while ensuring no worker is assigned more than one task.

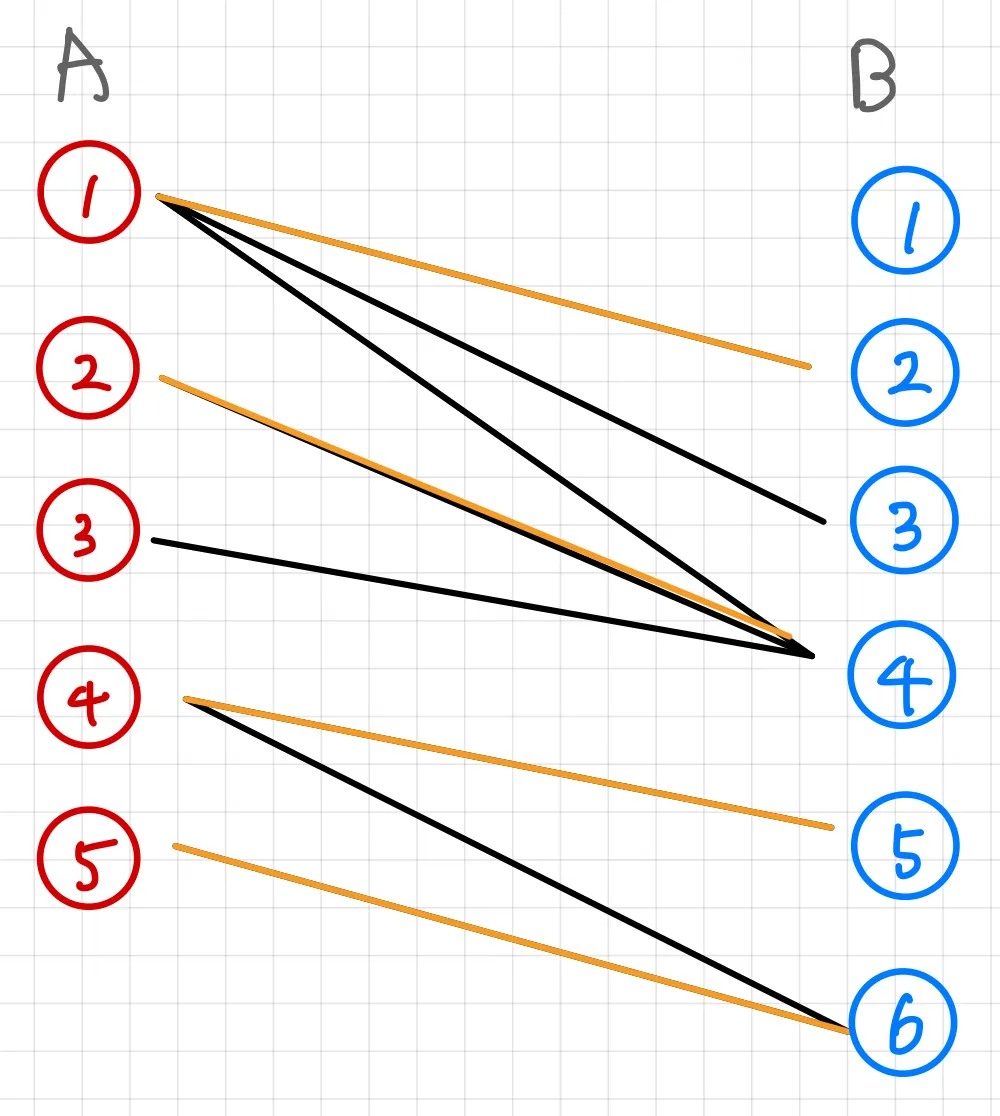
For example, the maximum bipartite matching is 4 in the above picture. Of course, another way of matching the edges can exist. You can match vertex 3 and vertex 4 instead of matching vertex 2 and vertex 4.

3. Algorithm Explanation

To be written…

4. Code

• If there exists an edge connecting vertex 1 in group A and vertex 2 in group B and an edge connecting vertex 1 in group A and vertex 3 in group B, we indicate this as 𝑉[1]={2,3}
• N represents the number of vertices in group A, and M represents the number of vertices in group B.
• The assign array indicates where a vertex in group B connects to in group A.
• The visit array tracks visiting history to prevent infinite loops.
• The time complexity is 𝑂(𝑁𝐸)(where 𝑁 is the number of vertices and 𝐸 is the number of edges).

bool dfs(int v,vector<vector<int>> &V, vector<bool> &visit, vector<int> &assign){
    for(auto to:V[v]){
        if(visit[to]) continue;
        visit[to]=true;

        if(assign[to]==0 || dfs(assign[to],V,visit,assign)){ 
            assign[to]=v;
            return true;
        }
    }
    return false;
}

int maximumBipartiteMatching(int N,int M,vector<vector<int>> & V){
    vector<bool> visit(M+1);
    vector<int> assign(M+1);
    int ans=0;
    for(int i=1; i<=N;i++){
        for(int j=1;j<=M;j++) visit[j]=0; 
        if(dfs(i,V,visit,assign)) ans++;
    }
    
    return ans;
}