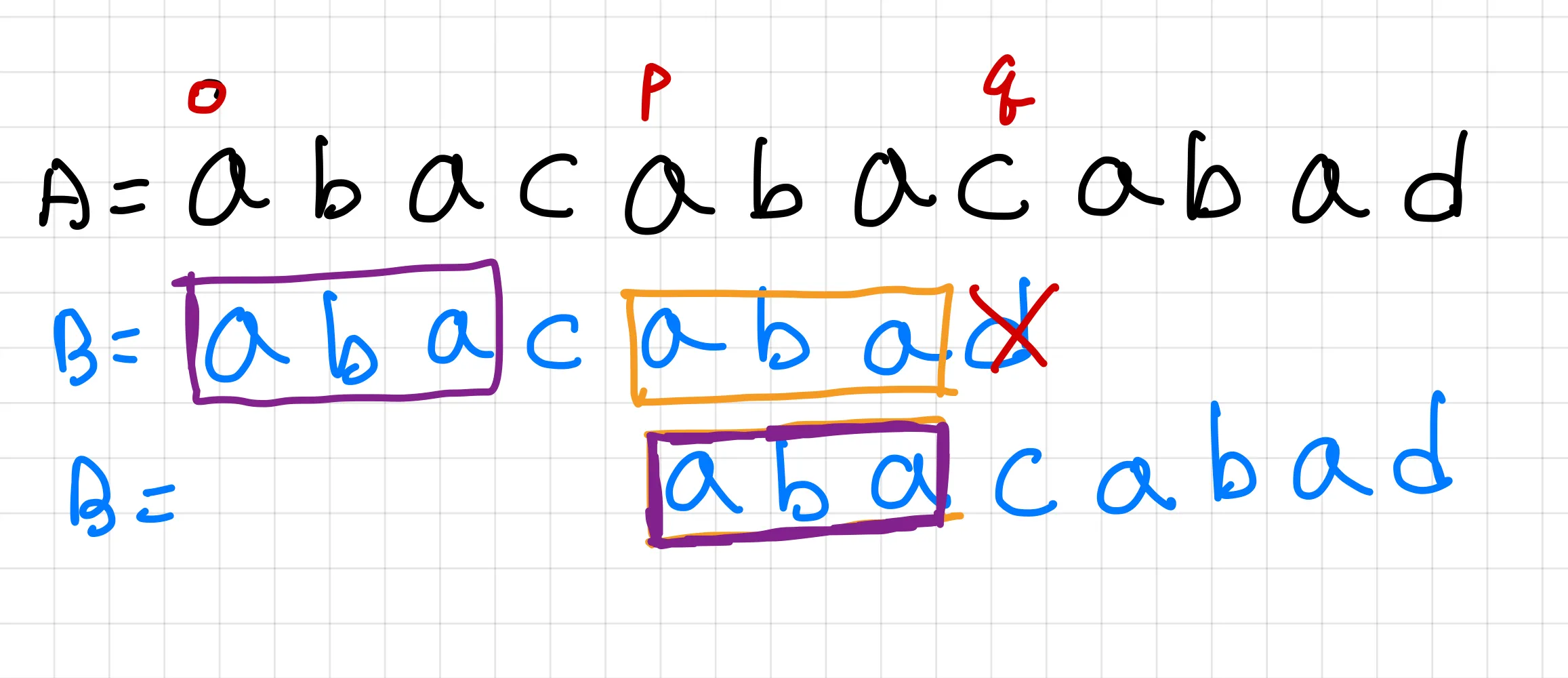KMP(Knuth-Morris-Pratt) Algorithm
The KMP (Knuth-Morris-Pratt) algorithm is a fast string search algorithm.
Referenced from 『프로그래밍 대회에서 배우는 알고리즘 문제 해결 전략 세트2』 p.657
1. Overview
Let’s suppose there are two strings, A and B. The length of A is N and the length of B is M. We can find out where B is included in A using the KMP algorithm. The time complexity of this algorithm is $\text{O(N + M)}$.
For example, if A is “abacabacabad” and B is “abacabad”, we can determine where B is included within A ( i=5 ) in $\text{O(length of A + length of B)}$ time complexity.
2. The Definition of the pi Array
Let’s define a substring of string B from index i to j as B[i…j].
pi[i] represents the maximum length of the string that can simultaneously serve as both a prefix and a suffix of the substring B[0…i].
The picture below will help you understand this definition.
Let’s temporarily set aside how to compute pi and assume that we have already constructed the pi array.
3. The Main Process of KMP
Let’s suppose there are two strings A( = “abacabacabad”) and B( = “abacabad”).
In $\text{O(N^2)}$ time complexity, you may write this code to find out where B is included in A.
1
2
3
4
5
6
7
8
9
10
vector<int> sample(string A, string B){
int N=A.size();
int M=B.size();
for(int i=0;i<=N-M;i++){
bool possible=true;
for(int j=0;j<M;j++)
if(A[i+j]!=B[j]) possible=false;
if(possible) printf("B is include within index: %d\n",i);
}
}
However, we don’t need to iterate from i=0 to i=N. What does this mean? Please refer to the explanation below.
Assuming we already have the pi array, when A[q] and B[q] do not match at i=0, the next step isn’t i=i+1 but rather i=p (where p = q - pi[q-1]). This transition is perfectly valid and crucial to understand. ( Here, pi[q-1] represents the maximum length of the string that can simultaneously serve as both a prefix and a suffix of “abacaba”. )
Furthermore, since A[p…(q-1)] = B[0…(p-q-1)], we can start comparing from A[q] and B[p-q].
Code: O(N)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
void kmp(string &A, string &B){
int N=A.size();
int M=B.size();
vector<int> whereBIsIncluded;
vector<int> pi = getPartialMatch(B); //Let's postpone the discussion on how this function is implemented for now.
int begin=0, matched=0;
while(begin<=N-M){
if(matched < M && A[begin+matched]==B[matched]){
++matched;
if(matched==M) whereBIsIncluded.push_back(begin);
} else{
if(matched==0) ++begin;
else {
begin += matched - pi[matched-1];
matched = pi[matched-1];
}
}
}
}
4. How to construct the pi array?
When constructing the pi array, we can utilize the same principle used in the previous explanation. We compute the pi[] array by leveraging the concept of self-matching appearances while searching for itself.
Code: O(M)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
vector<int> getPartialMatch(const string &B) {
int M = B.size();
vector<int> pi(M, 0);
int begin = 1, matched = 0;
while (begin + matched < M) {
if (B[begin + matched] == B[matched]) {
++matched;
pi[begin + matched - 1] = matched;
} else {
if (matched == 0) ++begin;
else {
begin += matched - pi[matched - 1];
matched = pi[matched - 1];
}
}
}
return pi;
}
5. Another Code: O(N+M)
This is an alternative implementation of KMP. The basic principle remains the same. It operates in O(N+M) time complexity.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
vector<int> getPartialMatch(string &B){
int M=(int)B.size(), matched=0;
vector<int> pi(M, 0);
for(int i=1;i<M;i++){
while(matched>0 && B[matched]!=B[i]) matched=pi[matched-1];
if(B[matched]==B[i]) pi[i]=++matched;
}
return pi;
}
void kmp(string &A, string &B){
int matched=0;
int N = (int)A.size(), M = (int)B.size();
vector<int> pi=getPartialMatch(B);
vector<int> whereBIsIncluded;
for(int i=0;i<N;i++){
while(matched>0 && A[i]!=B[matched])
matched=pi[matched-1];
if(A[i]==B[matched]){
++matched;
if(matched==M){
whereBIsIncluded.push_back(i-matched+1);
matched=pi[matched-1];
}
}
}
}
Next Post
If you understand what is kmp and how to construct it. I recommend read Z-algorithm